Le tri bulle

Le principe du tri à bulles (bubble sort ou sinking sort en anglais) est très simple : pour trier une liste, on compare son premier et son second élément et on les échange si nécessaire. Puis on fait la même chose pour le second et le troisième, puis pour le troisième et le quatrième… jusqu’à ce qu’on arrive à la fin de la liste. Après cela, on recommence à partir du début. Au bout d’un certain nombre d’itérations, on ne fait plus de permutations. Alors la liste est triée.

On remarque, qu’après le premier passage, l’élément le plus grand se retrouve à sa place définitive. Au deuxième passage, il sera donc inutile de le comparer avec le précédent. A chaque itération, on aura un élément de plus qui sera correctement placé à la fin de la liste. On pourra donc, à chaque fois, s’arrêter un peu plus tôt.

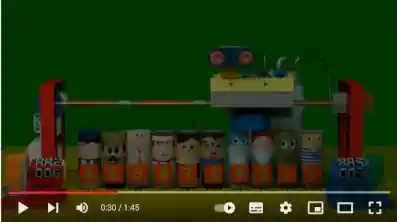
L’animation ci-dessous illustre le fonctionnement de ce tri.

1. void bubble_sort(int* lst, int size)
2. {
3.     int pass = 0;
4.     int swapped = 1;
5.     int current;
6.     while (swapped) {
7.         swapped = 0;
8.         pass ++;      
9.         for (current=0;current<size-pass;current++) {
10.         if (lst[current]>lst[current+1]){
11.             swapped = 1;
12.             // On permute les deux éléments
13.             int temp = lst[current];
14.             lst[current] = lst[current+1];
15.             lst[current+1] = temp;
16.         }
17.         }
18.     }
19. }

1. def bubble_sort(lst):
2.   swapped = True
3.   num_pass = 0
4.   while swapped == True:
5.     swapped = False
6.     num_pass = num_pass + 1
7.     for current in range(0, len(lst) - num_pass):
8.       if (lst[current] > lst[current + 1]):
9.         swapped = True
10.         # On echange les deux elements
11.         lst[current], lst[current + 1] = lst[current + 1],lst[current]
12.   return lst

1. type tab = array[1..20] of integer;
2. procedure bubble_sort(var lst : tab);
3.    
4. var swapped : boolean;
5.     current : integer;
6.     temp : integer;
7.     pass : integer;
8.      
9. begin
10.   pass := 1;
11.   REPEAT
12.     swapped := false;
13.     for current := 1 to 20 - pass do
14.     begin
15.     if (lst[current] > lst[current + 1]) then
16.     begin
17.         { on échange les deux éléments }
18.         temp := lst[current];
19.         lst[current]:=lst[current + 1];
20.         lst[current + 1]:=temp;
21.         swapped := true;
22.     end;
23.     end;
24.     pass := pass + 1;
25.     UNTIL (not swapped);
26. end;

1. let swap a b t =
2.     let temp = t .( b ) in t .( b ) <- t .( a ) ; t .( a ) <- temp ;;
3.  
4. let bubble_sort vect =
5.     let length = Array.length vect in
6.         for max_pos = length - 1 downto 0 do
7.             for current = 0 to max_pos - 1 do
8.                 if vect.( current ) > vect.( current &plus 1 ) then swap current ( current &plus 1 ) vect
9.             done;
10.         done;
11.     vect;
12. ;;

Vous trouverez ici une petite vidéo qui montre cet algorithme.

Travaux pratiques

Le mini-jeu ci-dessous vous permet d’essayer de trier, par ordre de poids croissant, une suite de 5 tonneaux, avec juste une balance pour les comparer. Vous pouvez essayer de le résoudre avec la méthode du tri bulle.

Variantes

La version originale de Donald Knuth est un peu plus simple, mais l’idée est la même : on compare les éléments adjacents et on échange si nécessaire. Elle se présentait ainsi :

void swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}
void bubble_sort(int* lst, int size) {
    for(int i=size-1; i > 0; i--)
        for(int j=0; j < i;j++)
            if (lst[j+1] < lst[j]){
                swap(&lst[j],&lst[j+1]);
            }
}

Toutefois, cette version a l’inconvénient de toujours faire le même nombre d’opérations, quel que soit le tableau en entrée. L’implémentation suivante s’arrête dès qu’elle a fait un parcours sans aucune permutation. C’est la plus courante aujourd’hui.

On peut encore l’améliorer un peu car, si dans une itération le dernier échange s’est fait à la position N, alors tous les éléments situés après cette position N sont dans le bon ordre. Donc, pour les itérations suivantes, il est inutile de les explorer à nouveau. Or aurait alors quelque chose comme ça :

void bubble_sort1(int* lst, int size)
{
    int swapped = 1;
    int lastswap = size ;
    int j;
    while (swapped) {
        swapped = 0;
        for (j=0;j<lastswap - 1;j++) {
            if (lst[j]>lst[j+1]){
                swapped = j+1;
                swap(&lst[j],&lst[j+1]);
            }
        }
        lastswap = swapped;
    }
}

Complexité

D’un point de vue pédagogique, cet algorithme est très intéressant. Il est facile à comprendre et donc tout aussi facile à expliquer. Il est facile à coder dans la plupart des langages informatiques et donne l’occasion de manipuler des vecteurs ou des listes. Il peut servir de base à de nombreux exercices d’optimisation . Et en plus, il a un nom sympa.

Mais, dans le monde réel, il faut bien dire qu’il n’est pas très performant. Il est souvent décrié, voire considéré comme “naïf” et à “à proscrire absolument”. Toutefois, il a quand même le mérite d’être suffisamment performant sur de petites listes ou des listes déjà partiellement triées.

Dans le pire des cas, avec des données triées à l’envers, les parcours successifs du tableau imposent d’effectuer (n² - n) / 2 échanges. Par exemple, pour une liste de 10 éléments, il faudra, dans le pire des cas, faire 45 comparaisons et 45 échanges [ (10² - 10) / 2 ]. La complexité en temps est donc quadratique, de l’ordre de O(n²).

En moyenne, lorsque l’ordre initial des éléments à trier est aléatoire, on considère qu’il faudra faire (n² - n) / 4 échanges. La complexité sera donc aussi de O(n²).

Dans le meilleur des cas, quand la liste est déjà triée, il faudra (n - 1) comparaisons et aucune permutation. La complexité en temps est linéaire, en O(n).

En espace utilisé (coût en mémoire de l’algorithme), la complexité du tri bulle est linéaire. Elle croit à la même vitesse que le nombre de données en entrée. Elle est donc de O(n).

L’animation ci-dessous permet de vérifier, de manière empirique, cette évolution du nombre d’opérations en fonction du nombre d’éléments à trier.

Pour vous faire une idée plus concrète des performances de cet algorithme, supposez que vous deviez trier par ordre alphabétique le répertoire des habitants de plusieurs grandes villes. Et que la machine dont vous disposez peut effectuer disons dix millions d’instructions par seconde (ce qui n’est pas si mal si on tient compte des problèmes d’accès à la mémoire, aux disques etc…). Voici le temps qui serait nécessaire avec cette méthode :

Vous pouvez changer le nombre d’instructions par seconde, pour tester.