Tri à peigne

19-12-2021
Tri à peigne
Le tri à peigne (Comb Sort en anglais) est un algorithme de tri par comparaison qui améliore de façon notable les performances du tri à bulle. Cet algorithme fut conçu en 1980 par Włodzimierz Dobosiewicz.
Il apporte une solution au problème des “lièvres” et des “tortues”. Les “lièvres”, sont les éléments de fin de liste qui migrent rapidement à leur place définitive et les “tortues” ceux de début de liste qui se déplacent lentement.
Plutôt que de toujours comparer des éléments adjacents, le tri à peigne va comparer des éléments séparés d’une distance plus grande. Au départ, on compare des éléments éloignés, puis on réduit progressivement l’intervalle à chaque itération jusqu’à ce qu’il ne soit plus que de 1 en fin de traitement. Le tri à bulles est donc un cas particulier du tri à peigne dans lequel l’intervalle est toujours de 1.
Cet algorithme est beaucoup plus performant que le tri bulle classique parce qu’il effectue davantage de comparaisons et d’échanges “à longue portée” ; la permutation de deux éléments qui sont éloignés l’un de l’autre permettra de les rapprocher beaucoup plus rapidement de leur position définitives que la permutation de deux éléments proches.
L’animation ci-dessous détaille le fonctionnement du tri à peigne :
Variantes
Complexité
La complexité du tri peigne est difficile à évaluer. Mais bon, je vais essayer. D’abord le meilleur des cas, avec une liste déjà triée ou pratiquement triée. Beaucoup d’articles sur le sujet disent que, dans le meilleur des cas, le tri peigne est plus performant que le tri bulle. C’est évidemment faux. Avec une liste déjà triée de disons 100 éléments, le tri bulle classique fera 99 comparaisons avant de s’arrêter. Le tri peigne fera une itération avec un gap de 76, puis une itération avec un gap de 58, puis avec un gap de 44… Et terminera avec un gap de 1. En tout, il fera 1003 comparaisons. Le graphique ci-dessous montre le nombre de comparaisons effectuées par un tri bulle classique (en bleu) et le tri peigne (en rouge) :
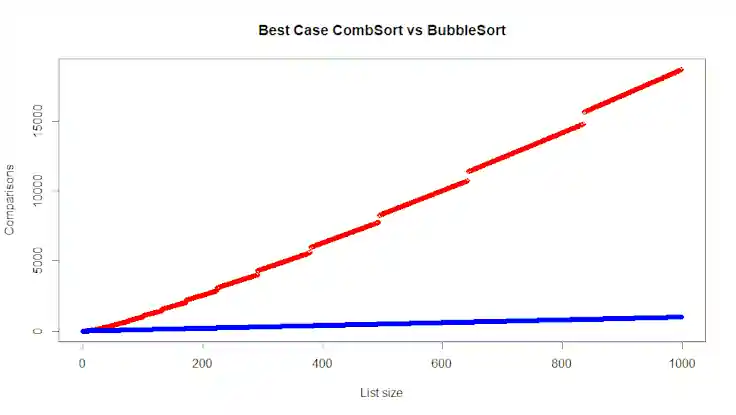
La forme “en escalier” de la courbe du tri Combsort provient du nombre d’incréments qui évolue en fonction de la taille des données à trier.
Pour la complexité moyenne, j’ai lu un papier d’un certain Paul VITANYI qui étudiait la complexité des différents tris basés sur la complexité de Kolmogorov mais j’avoue ne pas avoir tout bien compris. Et surtout, expérimentalement, je ne trouve pas du tout les mêmes résultats. M. Vitanyi annonce une compléxité de omega (n^2/2^p) avec p, le nombre d’incréments. On peut dire que p est égal à ln(N)/ln(1.3) (avec N le nombre d’éléments à trier et un facteur de réduction de 1.3). Donc, avec N=10 on aurait 8 incréments (le nombre est un peu sur-évalué parce qu’en pratique, on arrondi à l’entier inférieur, mais bon) et 0.390625 comparaisons. Ok, c’est une borne inférieure, et il faudrait la multiplier par une constante. Le plus embêtant, c’est que, plus la taille des données augmente, plus le calcul n^2/2^p diminue :
| Nombre d’éléments | Nombre d’incréments | Nombre d’opérations |
|---|---|---|
| 10 | 8 | 0.390625 |
| 100 | 17 | 0.07629345 |
| 1000 | 26 | 0,014901161 |
| 100 000 | 43 | 0,001136868 |
| 500 000 | 50 | 0,000222045 |
| 1 000 000 | 52 | 0,000222045 |
Est-ce que cela signifie que le nombre d’opération évolue de manière inverve avec la taille des données à trier ? C’est évidemment absurde et j’ai dû me tromper quelque part.
J’ai donc lancé l’algorithme avec quelques 100 000 jeux de données aléatoires (d’une taille entre 10 et 500 000 éléments) et j’ai ensuite analysé les résultats avec R. En moyenne, la complexité serait plutôt de 3log2(N)N (avec N, la taille du vecteur à trier). Enfin, j’ai créé un tableau avec 42 796 714 (le nombre d’habitants de Tokyo) entiers aléatoires que j’ai trié avec cette méthode. Là encore, les résultats sont très proches de l’estimation 3log2(N)N et surtout étonnement rapides pour un algorithme aussi simple.
Le graphique suivant donne le nombre de comparaisons pour 21255 listes aléatoires de tailles comprises entre 10 et 100 000 éléments. En bleu, la courbe d’équation y=log2(x)x. La quasi-totalité des mesures se situe sous la courbe. Même si ça ne prouve rien, il semblerait que 3log2(N)*N serait une borne supérieure pour la complexité en moyenne.
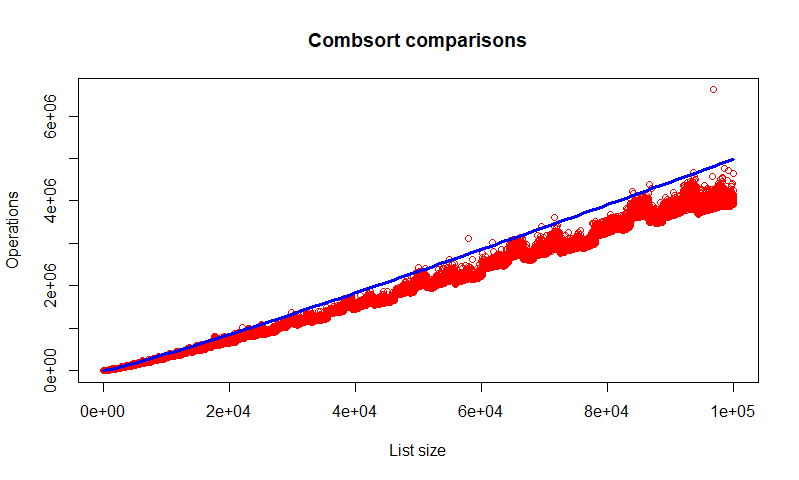
Enfin, la complexité dans le pire des cas me pose un autre problème. Pour ce tri, le pire des cas n’est pas la liste triée en ordre inverse. Par exemple, le tri de la liste [5,4,3,2,1] nécessitera 13 comparaisons et 4 échanges tandis que celui de la liste [5,2,3,4,1] demandera 13 comparaisons et 7 échanges.
La comparaison avec le tri bulle est assez explicite. Le graphique ci-dessous montre le nombre de comparaisons effectuées par un tri bulle (en rouge) et par un tri à peigne (en bleu).
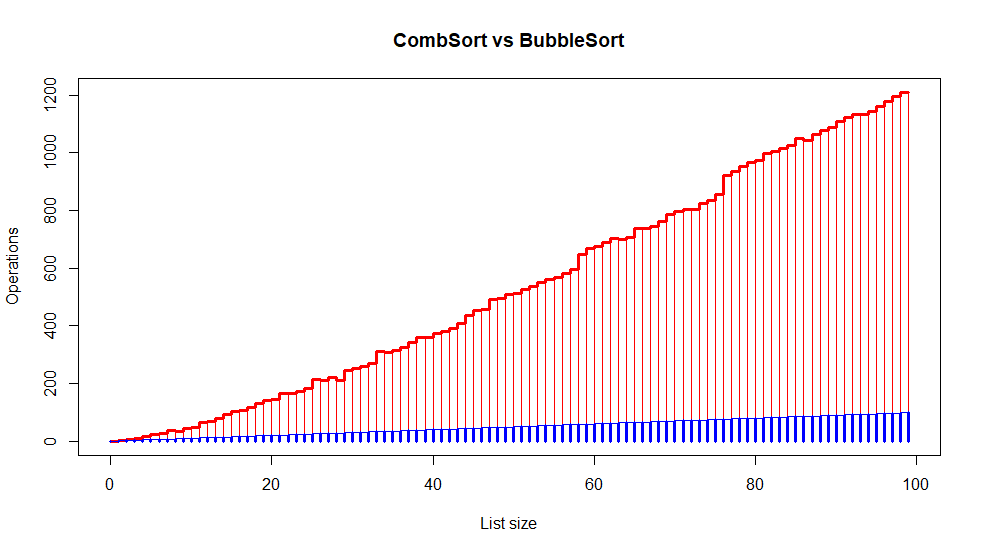
| Taille données | Comparaisons | Echanges | Total |
|---|
Pour vous faire une idée plus concrète des performances de cet algorithme, supposez que vous deviez trier par ordre alphabétique le répertoire des habitants de plusieurs grandes villes. Et que la machine dont vous disposez peut effectuer disons dix millions d’instructions par seconde. Voici le temps qui serait nécessaire avec cette méthode :
| Ville | Nombre d'habitants | Estimation de la durée du tri |
|---|---|---|
| Churriana de la Vega | 16 689 | |
| Helsinki | 631 695 | |
| Palerme | 673 735 | |
| Stockholm | 975 551 | |
| Berlin | 3 520 031 | |
| Nairobi | 4 734 881 | |
| Saint-Pétersbourg | 5 131 942 | |
| Rio | 6 718 000 | |
| Bombay | 18 414 288 | |
| Lagos | 22 829 561 | |
| Shanghai | 24 870 895 | |
| Séoul | 26 000 782 | |
| Manille | 28 644 207 | |
| Tokyo | 42 796 714 |


