The Bubble Sort

2021-11-20
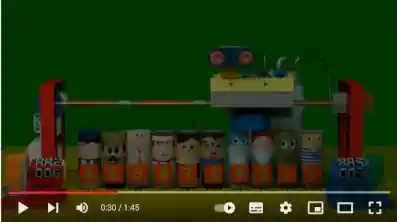
Visual of the 'bubble sorting' algorithm
Bubble sort (aka sinking sort) is a sorting algorithm that works by repeatedly stepping through the list that need to be sorted, comparing each adjacent pair of items and swapping them if necessary.
This procedure is repeated until no swaps are done.
Since at least one item is moved into its final place for each pass, we can decrement the last position checked on each pass.
The animation below shows how the bubble sort works :
you will find here here a short video illustrating this algorithm.
Practical work
The mini-game below allows you to try to sort, in order of increasing weight, 5 barrels, with a Roberval scale to compare them. You can try to solve it with the bubble sort method.
Variations
Donald Knuth’s original version is a bit simpler, but the idea is the same: we compare adjacent elements and exchange if necessary.
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void bubble_sort(int* lst, int size) {
for(int i=size-1; i > 0; i--)
for(int j=0; j < i;j++)
if (lst[j+1] < lst[j]){
swap(&lst[j],&lst[j+1]);
}
}
However, this version has the disadvantage that it always performs the same number of operations, regardless of the input array. The next implementation stops as soon as it has done a run without any permutation. This is the most common one today.
We can still improve it a little because, if in an iteration the last exchange was done at position N, then all the elements located after this position N are in the right order. So, for the following iterations, it is useless to explore them again. We would then have something like this:
void bubble_sort1(int* lst, int size)
{
int swapped = 1;
int lastswap = size ;
int j;
while (swapped) {
swapped = 0;
for (j=0;j<lastswap - 1;j++) {
if (lst[j]>lst[j+1]){
swapped = j+1;
swap(&lst[j],&lst[j+1]);
}
}
lastswap = swapped;
}
}
Complexity
From an educational point of view, this algorithm is very interesting. It is easy to understand and therefore also easy to explain. It is easy to write and debug in most computer languages and gives the opportunity to manipulate vectors or lists. It can be used as a basis for many optimization exercises. And it has a catchy name.
But, in the real world, it must be said that it is not very efficient. It is often decried, even considered as “naive” and “to be avoided absolutely”. However, it has the merit of being sufficiently efficient on small lists or lists that are already partially sorted.
In the worst case, with data sorted in reverse, the successive runs of the table require (n2 - n) / 2 exchanges. For example, for a list of 10 items, it will take, in the worst case, 45 comparisons and 45 exchanges [ (102 - 10) / 2 ]. The time complexity is therefore quadratic, of the order of O(n2).
When the initial order of the items to be sorted is random, it is considered that (n2 - n) / 4 exchanges will be needed. The complexity will therefore also be O(n2).
In the best case, when the list is already sorted, it will take (n - 1) comparisons and no permutations. The time complexity is linear, in O(n).
In terms of space used (memory cost of the algorithm), the complexity of the bubble sort is linear. It grows at the same speed as the number of input data. It is therefore O(n).
The animation below allows to verify, in an empirical way, this evolution of the number of operations according to the number of elements to sort.
| Data size | Comparisons | Exchanges | Total |
|---|
To get a more concrete idea of the performance of this algorithm, suppose that you have to sort alphabetically the directory of the inhabitants of several large cities. And that the machine you have at your disposal can perform, say, ten million instructions per second . Here is the time that would be needed with this method:
| City | Population | Estimated sorting time |
|---|---|---|
| Chicoutimi | 69 004 | |
| Brussels | 174 383 | |
| Paris | 2 220 445 | |
| Madrid | 3 207 247 | |
| Berlin | 3 520 031 | |
| Toronto | 6 555 205 | |
| London | 8 416 535 | |
| Mexico | 20 879 830 | |
| Cairo | 24 439 785 | |
| Delhi | 26 454 086 | |
| Jakarta | 35 143 473 | |
| Sao Paulo | 36 315 271 | |
| Tokyo | 42 796 714 |