Tri par insertion

C’est le tri du joueur de cartes. On fait comme si les éléments à trier étaient donnés un par un, le premier élément constituant, à lui tout seul, une liste triée de longueur 1. On range ensuite le second élément pour constituer une liste triée de longueur 2, puis on range le troisième élément pour avoir une liste triée de longueur 3 et ainsi de suite… Le principe du tri par insertion est donc d’insérer à la nième itération le nième élément à la bonne place.

L’animation ci-dessous détaille le fonctionnement de ce tri :

void InsertionSort(int vect[], int size)
{
    int i, current, j;
    for (i = 1; i < size; i++) {
        current = vect[i];
        j = i - 1;
        while (j >= 0 && vect[j] > current) {
            vect[j + 1] = vect[j];
            j = j - 1;
        }
        vect[j + 1] = current;
    }
}

def InsertionSort(vect):
    for i in range(1, len(vect)):
        current = vect[i]
        p = i
        while p > 0 and vect[p - 1] > current:
            vect[p] = vect[p -1]
            p = p - 1
        vect[p] = current

function InsertionSort(lst) {
	let size = lst.length;
        for (let i = 1; i < size; i++) {            
            let current = lst[i];            
            let j = i-1; 
            while ((j > -1) && (current < lst[j])) {
                lst[j+1] = lst[j];
                j--;
            }
            lst[j+1] = current;
        }
    return lst;
}

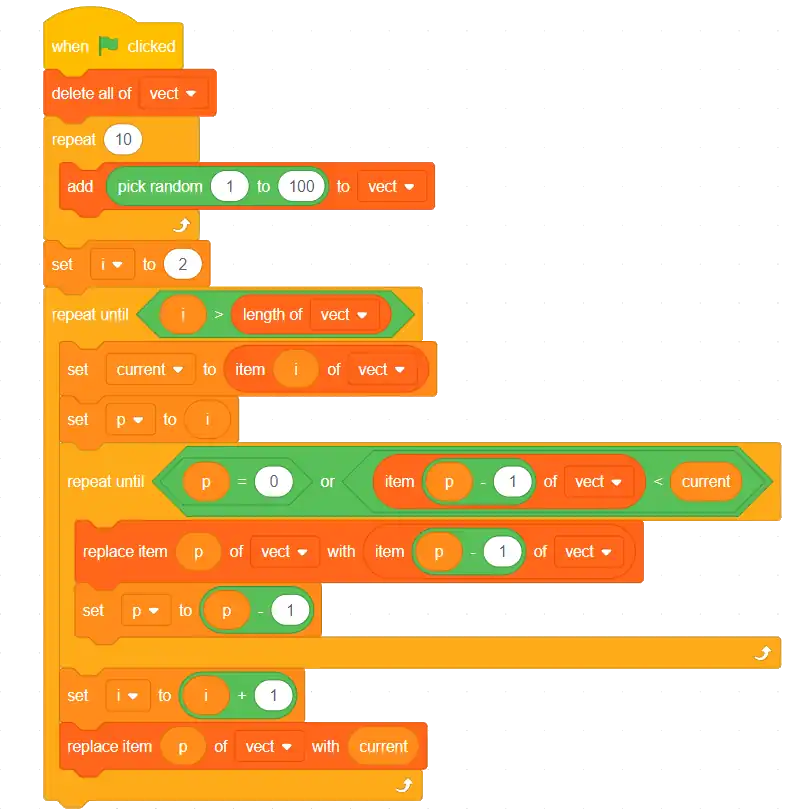
Implémentation

Ci dessous, une version simple de cet algorithme, en python.

Complexité

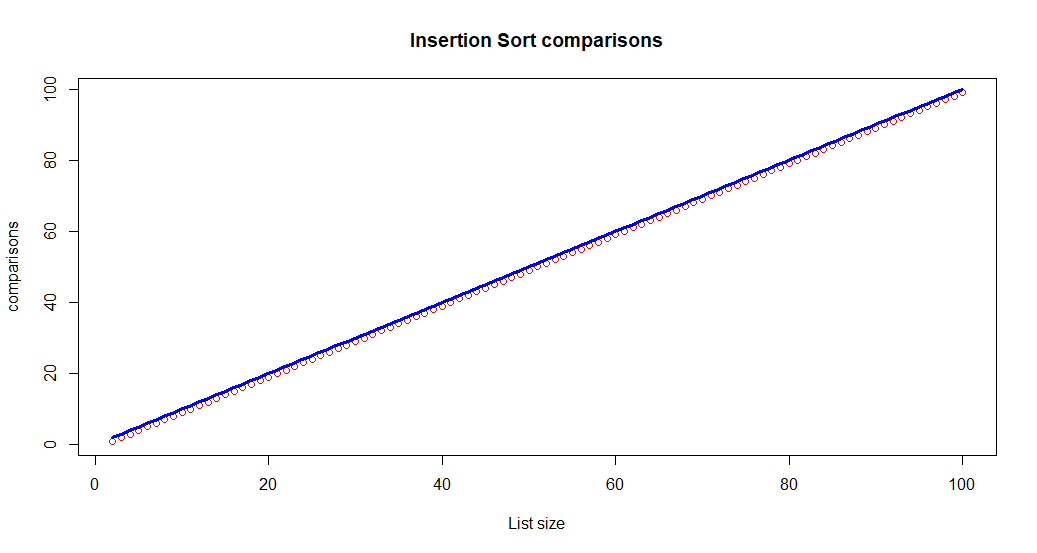
Dans le meilleur des cas (c’est à dire avec une liste déjà triée), le tri par insertion fera exactement n-1 comparaisons, n étant le nombre d’éléments de la liste. C’est assez intuitif : si la liste à trier ne contient qu’un élément, il ne fera aucune comparaisons, si elle en contient deux, une comparaison suffira, si elle en contient 3 deux comparaisons seront nécessaires… La complexité en temps est linéaire, en O(n).

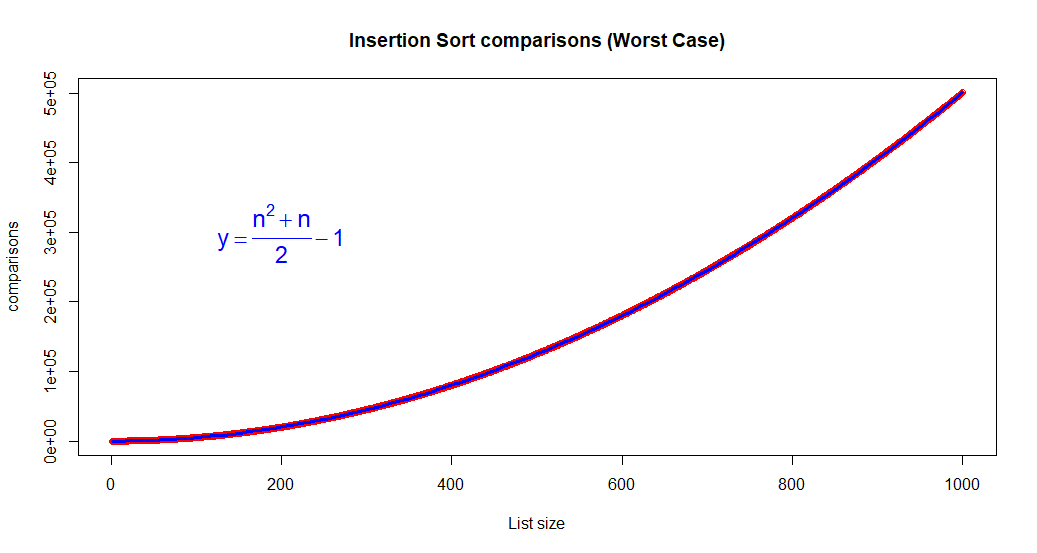
Dans le pire des cas (c’est à dire avec une liste triée en sens inverse) le tri par insertion fera exactement (n^2+n)/2 - 1 opérations, n étant le nombre d’éléments de la liste (ce qu’on peut aussi écrire “n(n+1)/2 - 1”. La complexité en temps est quadratique, en O(n²). Le graphique suivant illustre cela :

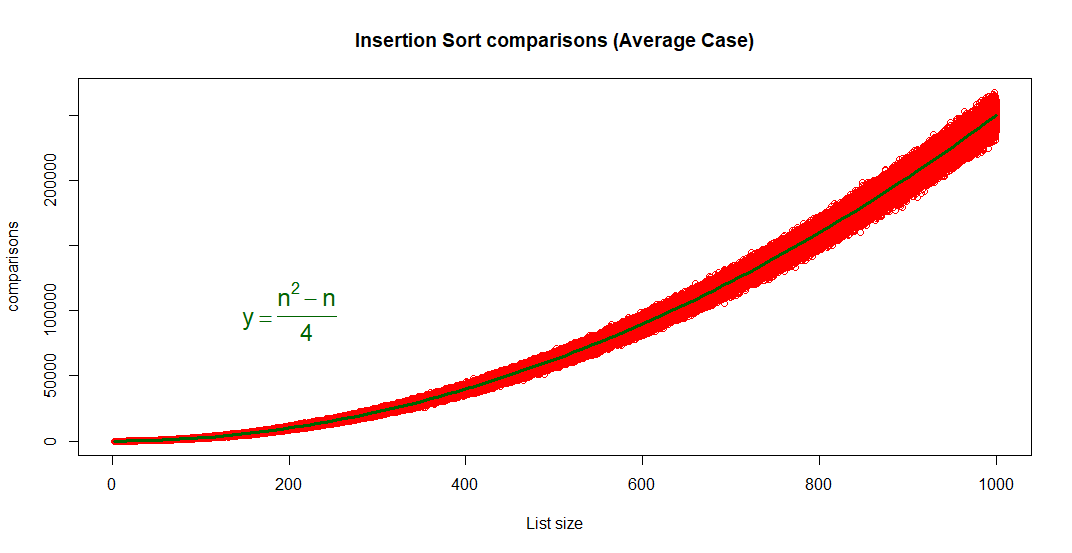
En moyenne, il faudra (n^2-n)/4 opérations pour trier une liste, soit un nombre d’opérations équivalent à celui nécessaires avec le tri bulle. Le graphique suivant a été réalisé en triant 1 217 818 listes (!) générées aléatoirement et en analysant le résultat avec R. Cela permet de vérifier que la complexité en temps est bien quadratique en moyenne.